Inverse Functions: One to One
DEFINITION OF ONE-TO-ONE:
A function is said to be one-to-one if each x-value corresponds to exactly one y-value.
A function f has an inverse function, f -1, if and only if f is one-to-one.
A quick test for a one-to-one function is the horizontal line test. If a horizontal line intersects the graph of the function in more than one place, the functions is NOT one-to-one.
HORIZONTAL LINE TEST:
A function f is one-to-one and has an inverse function if and only if no horizontal line intersects the graph of f at more than one point.
Let's use this characteristic to determine if a function has an inverse.
|
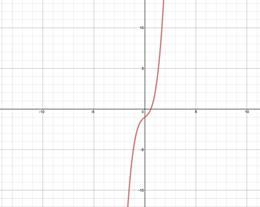
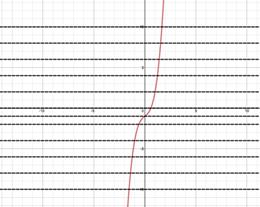
Step 1: Sketch the graph of the function. |
|
|
Step 2: Apply the Horizontal Line Test. Visualize multiple horizontal lines and look for places where the graph is intersected more than once. No horizontal line intersects the graph in more than one place and thus the function has an inverse. |
|
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
y |
5 |
0 |
-3 |
-4 |
-3 |
0 |
5 |
|
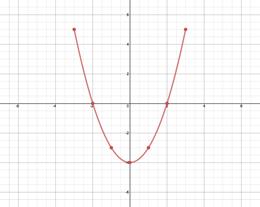
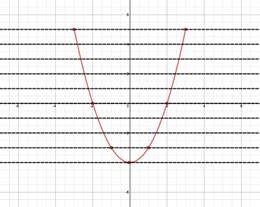
Step 1: Sketch the graph of the function. |
|
||||||||||||||||
|
Step 2: Apply the Horizontal Line Test. Visualize multiple horizontal lines and look for places where the graph is intersected more than once. Several horizontal lines intersect the graph in two places. Thus the function is not a one-to-one and does not have an inverse. Also notice that if the ordered pairs are switched, this results in repeating x-values and a function cannot have repeating x-values.
|
|
|
Related Links: Math algebra Inverse Functions: Finding Inverse Functions Analytically Conics: Classifying from General Equation Pre Calculus |
To link to this Inverse Functions: One to One page, copy the following code to your site: