Home > Math > Pre Calculus > Parabola: Standard Equation

Parabola: Standard Equation

A parabola is a conic section that is described as:

DEFINITION OF A PARABOLA:


The set of all points (x, y) in a plane that are the same distance from a fixed line, called the directrix, and a fixed point or focus not on the directrix.





Figure 1 shows a picture of a parabola



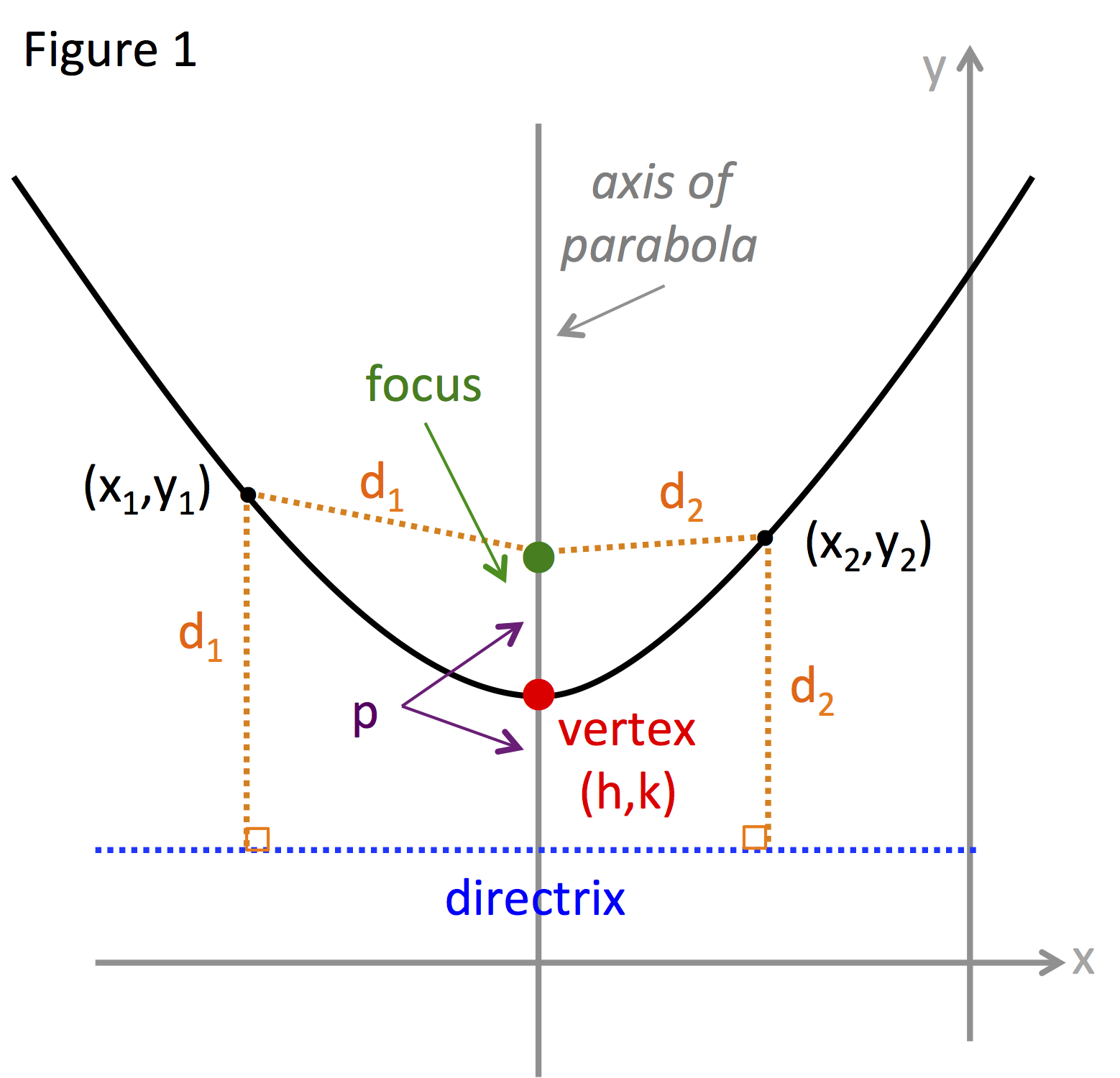
Notice that the distance from the focus to point (x1, y1) is the same as the line perpendicular to the directrix, d1.

The midpoint between the directrix and the focus falls on the parabola and is called the vertex of the parabola.

The line that passes through the focus and the vertex is called the axis of the parabola. The parabola in the figure has a vertical axis however it is possible for a parabola to have a horizontal axis.

The standard equation of a parabola is:

STANDARD EQUATION OF A PARABOLA:


Let the vertex be (h, k) and p be the distance between the vertex and the focus and p ≠ 0.


( x−h ) 2 =4p( y−k ) vertical axis; directrix is y = k - p


( y−k ) 2 =4p( x−h ) horizontal axis; directrix is x = h - p




Let's use these equations in some examples:

Example 1: Find the standard equation of the parabola with vertex at (4, 2) and focus at (4, -3).

Step 1: Determine the following:


➢ the coordinates of the vertex (h, k).


➢ the orientation of the axis.


➢ the distance between the focus and the vertex (p).

Vertex:

(h, k) = (4, 2) Given


Axis orientation: Both the focus and the vertex fall on the axis. Looking at their coordinates reveals that both fall on the vertical line x = 4. Thus the axis of the parabola is vertical.


Distance between focus and vertex: Since both focus and vertex fall on the vertical line x = 4 determine the distance between the point by subtracting their y-coordinates and taking the absolute value.


| y f − y v |=| −3−2 |=| −5 |=5=p

Step 2: Substitute the values for h, k and p into the equation for a parabola with a vertical axis.

(x - h)2 = 4p(y - k) Vertical axis


( x−4 ) 2 =4( 5 )( y−2 ) Sub


( x−4 ) 2 =20( y−2 ) Simplify

Example 2: Find the standard equation of the parabola with vertex at
(4, 1) and directrix of x = -3.

Step 1: Determine the following:


➢ the coordinates of the vertex (h, k).


➢ the orientation of the axis.


➢ the distance between the focus and the vertex (p).

Vertex:


(h, k) = (4, 1) Given


Axis orientation: The directrix is always perpendicular to the axis. Since the directrix is given as x = -3, a vertical line, the axis is a horizontal line.


Distance between focus and vertex, p : The vertex is the midpoint of the focus and the directrix. Therefore the distance from the vertex to the directrix is the same as the distance from the vertex to the focus. To find the distance from the vertex to the directrix find the absolute value of the change between their x-coordinates.


| x v − x d |=| 4−( −3 ) |=| 7 |=7

Step 2: Substitute the values for h, k and p into the equation for a parabola with a horizontal axis.

( y−k ) 2 =4p( x−h )


( y−1 ) 2 =4( 7 )( x−4 )


( y−1 ) 2 =28( x−4 )





Related Links:
Math
algebra
Ellipse: Standard Equation
Ellipse: Eccentricity
Pre Calculus


To link to this Parabola: Standard Equation page, copy the following code to your site: