Parametric Equations: Eliminating Parameters

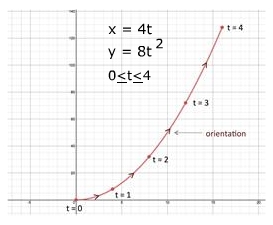
To sketch the graph of parametric equations, x and y coordinates must be obtained. This can be accomplished by selecting values for the parameter and calculating the x- and y-values one at a time. This process, called point plotting, works well when given a small finite interval for the parameter.

x = 4t, y = 8t², when $0 \leq t \leq 4$

Time, t

Distance, x

x = 4t

Height, y

y = 8t²

128

When the interval is not small and finite, point plotting becomes tedious and does not always reveal the overall behavior of the graph. Curve sketching can be less tedious by converting the two parametric equations into one rectangular equation. This method is referred to as eliminating the parameter.

To eliminate the parameter, solve one of the parametric equations for the parameter. Then substitute this result for the parameter in the other parametric equation and simplify.

GUIDELINES FOR ELIMINATING THE PARAMETER:

1. Solve one parametric equation in terms of the parameter.

2. Substitute the resulting expression for the parameter into the other parametric equation.

3. Simplify

Let's use this method on the pair of parametric equations above. Solve one of the parametric equations for the parameter, say x = 4t.

$x = 4 t \to \frac{x}{4} = t$

Substitute the resulting expression for the parameter into the other parametric equation and simplify.

$y = 8 t^{2} \to y = 8 {(\frac{x}{4})}^{2} \to y = \frac{8 x^{2}}{16} \to y = \frac{x^{2}}{2}$

The resulting rectangular equation,

\frac{1}{2} x^{2}

, represents a parabola that opens up, has an axis of symmetry at x = 0 and a vertex of (0, 0).

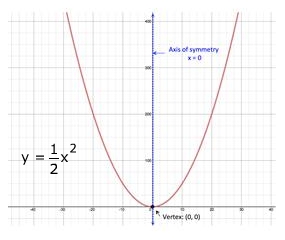
See how this rectangular equation gives a better understand of the curve as a whole.

Understand that eliminating the parameter is just a way to understand the overall behavior of the curve. The parametric equations are still necessary to describe the parameter and the orientation of the curve.

One caution when eliminating the parameter, the domain of the resulting rectangular equation may need to be adjusted to agree with the domain of the parameter as given in the parametric equations.

In the example above, the domain of the parameter t in both parametric equations is the set of all real numbers, x = 4t and y = 8t². The domain of the rectangular equation,

y = \frac{1}{2} x^{2}

, is also the set of real numbers. Since the domain is the same for both the parameter and the rectangular equation no domain adjustments are required.

Look at the following set of parametric equations:

x = t + 3

y = t - 49

Solve the first parametric equation for the parameter.

$x = \sqrt{t} + 3 \to x - 3 = \sqrt{t} \to {(x - 3)}^{2} = t$

Substitute the resulting expression for the parameter into the other parametric equation and simplify.

y = t - 49

y = (x-3)² - 49

y = (x² - 6x + 9) - 49

y = x² - 6x + 40

Based on the resulting rectangular equation, y = x² - 6x + 40, the domain is all real numbers. However, the parametric equation,

x = \sqrt{t} + 3

, limits the domain of t to numbers where t > 0. Therefore the domain of the rectangular equation, y = x² - 6x + 40, must be restricted to all numbers where x > 0.

Let's try a couple of examples.

Example 1: Eliminate the parameter and obtain the rectangular equation, state the domain and sketch the curve for the pair of parametric equations.

$x = t^{2} - 4$ $y = 3 t^{2} + 5$

Step 1: Solve one of the parametric equations for the parameter	x = t² - 4 Original x + 4 = t² Add 4 $\pm \sqrt{x + 4} = t$ Take square root
Step 2: Substitute the resulting expression for the parameter into the other parametric equation and simplify.	$y = 3 t^{2} + 5$ Other equation $y = 3 {(\pm \sqrt{x + 4})}^{2} + 5$ Substitute for t $y = 3 (x + 4) + 5$ Square $y = 3 x + 12 + 5$ Multiply/Distribute $y = 3 x + 17$ Add
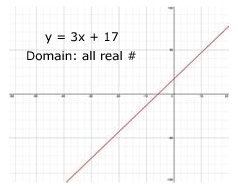
Step 3: Determine the domain of the rectangular equation.	The domain for t in both parametric equations is all real numbers and the domain for x in the rectangular equation is all real numbers. Thus no adjustments are need to the domain of the rectangular equation. Domain: All real numbers
Step 4: Sketch the curve.

Example 2: Eliminate the parameter and obtain the rectangular equation, state the domain and sketch the curve for the pair of parametric equations.

x = \frac{1}{t + \frac{1}{2}}

y = \frac{1}{t^{2}} + 10

Step 1: Solve one of the parametric equations for the parameter	$x = \frac{1}{t + \frac{1}{2}}$ Original $\frac{1}{x} = t + \frac{1}{2}$ Take inverse $\frac{1}{x} - \frac{1}{2} = t$ Subtract 1/2
Step 2: Substitute the resulting expression for the parameter into the other parametric equation and simplify.	$y = \frac{1}{t^{2}} + 10$ Other equation $y = \frac{1}{{(\frac{1}{x} - \frac{1}{2})}^{2}} + 10$ Substitute for t $y = \frac{1}{\frac{1}{x^{2}} - \frac{1}{x} + \frac{1}{4}} + 10$ Square denom. $y = x^{2} - x + 4 + 10$ x by reciprocal $y = x^{2} - x + 14$ Add
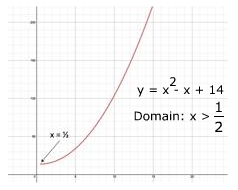
Step 3: Determine the domain of the rectangular equation.	The domain for t in the first parametric equation, $x = \frac{1}{t - \frac{1}{2}}$ , is $t > \frac{1}{2}$ . The domain for t in the second parametric equation, $y = \frac{1}{t^{2}} + 10$ is $t > 0$ . To meet both constraints, the domain of t must be $t > \frac{1}{2}$ . Therefore the domain of the rectangular equation, $x^{2} - x + 14$ , is $x > \frac{1}{2}$ Domain: $x > \frac{1}{2}$
Step 4: Sketch the curve.

To link to this Parametric Equations: Eliminating Parameters page, copy the following code to your site:

<a href="https://www.softschools.com/math/pre_calculus/parametric_equations_eliminating_parameters/">Parametric Equations: Eliminating Parameters</a>

Parametric Equations: Eliminating Parameters

More Topics

Educational Videos