Finding Parametric Equations for a Graph

A set of parametric equations is not unique for a given graph. For example the following sets of parametric equations result in the same rectangular equation and thus represent the same graph.

First Parametric equation

Second Parametric Equation

Rectangular Equation

$x = 4 t^{2} - 4$

y = t

$x = 4 y^{2} - 4$

$x = t^{2} - 4$

$y = \frac{t}{2}$

2y = t

x = (2y)² - 4

$x = 4 y^{2} - 4$

However, given a rectangular equation and an equation describing the parameter in terms of one of the two variables, a set of parametric equations can be determined.

To find a set of parametric equations for the graph represented by y = x² + 2 given t = x + 2, let t = x. Switching the roles of t and x in this equation gives one of the parametric equations:

$t = x + 2 \to x = t + 2$

Now substitute the expression for x into the rectangular equation, y = x² + 2 to obtain the second parametric equation.

$y = x^{2} + 2$

$y = {(t + 2)}^{2} + 2$

$y = t^{2} + 4 t + 4 + 2$

$y = t^{2} + 4 t + 6$

Thus the set of parametric equations for the graph represented by y = x² + 2 is,

$x = t + 2$

$y = t^{2} + 4 t + 6$

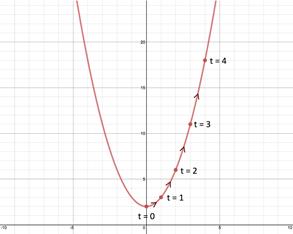
Now that both parametric equations have been determined, the overall graph can be drawn with selected values for the parameter.

t	-2	-1	0	1	2
x = t + 2	0	1	2	3	4
y = t² + 4t + 6	2	3	6	11	18

GUIDELINES FOR FINDING THE PARAMETRIC EQUATIONS FOR A GRAPH:

1. Take the parameter equation and switch the roles of the parameter and the other variable. This will result in one parametric equation.

2. Substitute the expression for the variable in Step 1 into the rectangular equation. This will result in the second parametric equation.

3. Sketch the curve.

Let's try a couple of examples.

Example 1: Find a set of parametric equations for the rectangular equation y = x² + 1, given t = 2 - x. Then sketch a graph locating points at $0 \leq t \leq 3$ and indicate the orientation of the curve.

Step 1: Take the parameter equation and switch the roles of the parameter and the other variable.

Let t = x and rewrite the parameter equation by switching t and x.

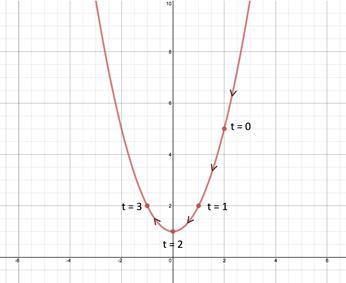
t = 2 - x Original

x = 2 - t Switch t and x

Step 2: Substitute the expression for the variable in Step 1 into the rectangular equation

$y = x^{2} + 1$ Original

$y = {(2 - t)}^{2} + 1$ Substitute

$y = (4 - 4 t + t^{2}) + 1$ Square

$y = 5 - 4 t + t^{2}$ Add

Step 3: Sketch the curve.

List the two parametric equations and sketch a graph locating points at $0 \leq t \leq 3$ and indicate the orientation of the curve.

Rectangular Equation: $y = x^{2} + 1$

Parametric Equations: x = 2 - t, $y = 5 - 4 t + t^{2}$

x = 2 - t

-1

y = 5 - 4t + t²

Example 2: Find a set of parametric equations for the rectangular equation $y = \frac{2}{x^{2} + 1}$ , given $t = \sqrt{x}$ . Then sketch a graph locating points at t = {0,1,2,3,4} and indicate the orientation of the curve.

Step 1: Take the parameter equation and switch the roles of the parameter and the other variable.

$t = \sqrt{x}$ Original

$x = \sqrt{t}$ Switch t and x

Step 2: Substitute the expression for the variable in Step 1 into the rectangular equation

$y = \frac{2}{x^{2} + 1}$ Original

$y = \frac{2}{{\sqrt{t}}^{2} + 1}$ Substitute

$y = \frac{2}{t + 1}$ Square

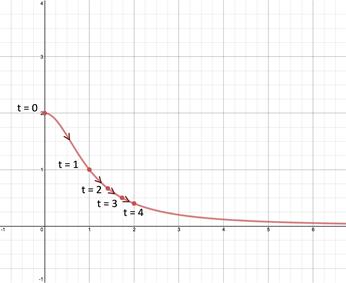
Step 3: Sketch the curve.

List the two parametric equations and sketch a graph locating points at t = {0, 1, 2, 3, 4} and indicate the orientation of the curve.

Rectangular Equation: $y = \frac{2}{x^{2} + 1}$

Parametric Equations: $x = \sqrt{t}$ , $y = \frac{2}{t + 1}$

$x = \sqrt{t}$

$\sqrt{2}$

$\sqrt{3}$

$y = \frac{2}{t + 1}$

$\frac{2}{3}$

$\frac{1}{2}$

$\frac{2}{5}$

Note that the domain of the graph is $x \geq 0$ because the domain of the parametric equation, $t = \sqrt{x}$ , limits x to values of zero or greater.

Related Links:
Math
algebra
Parametric Equations: Derivatives
Inverse Functions: Graphs
Pre Calculus

To link to this Finding Parametric Equations for a Graph page, copy the following code to your site:

<a href="https://www.softschools.com/math/pre_calculus/finding_parametric_equations_for_a_graph/">Finding Parametric Equations for a Graph</a>

Finding Parametric Equations for a Graph

More Topics

Educational Videos