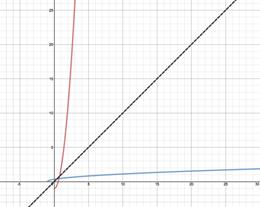
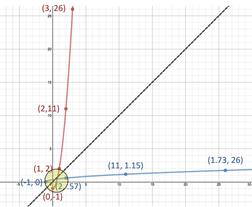
Inverse Functions: Graphs

A feature of a pair of inverse function is that their ordered pairs are reversed. For example

f (x) = 2 x + 1

and its inverse function,

f^{- 1} (x) = \frac{x - 1}{2}

, have the following ordered pairs:

f(x) = 2x + 1: (0, 1), (1, 3), (2, 5), (3, 7)

$f^{- 1} (x) = \frac{x - 1}{2}$ : (1, 0), (3, 1), (2, 5), (7, 3)

When graphed the functions will be a reflection of the other over the line y = x as shown below.

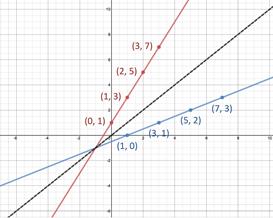
GRAPHS OF INVERSE FUNCTIONS:

Inverse functions have graphs that are reflections over the line y = x and thus have reversed ordered pairs.

Let's use this characteristic to identify inverse functions by their graphs.

GUIDELINES FOR FINDING IDENTIFYING INVERSE FUNCTIONS BY THEIR GRAPHS:

1. Sketch both graphs on the same coordinate grid.

2. Draw the line y = x and look for symmetry.

a. If no symmetry is apparent, the functions are not inverse functions.
b. If symmetry is apparent, go to Step 3 to verify.

3. Compare the coordinates of at least four points to determine if they are reversed. If so the functions are inverses.

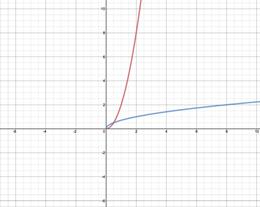
Example 1: Sketch the graphs of f(x) = 2x² and $g (x) = \sqrt{\frac{x}{2}}$ for $x \geq 0$ and determine if they are inverse functions.

Step 1: Sketch both graphs on the same coordinate grid.

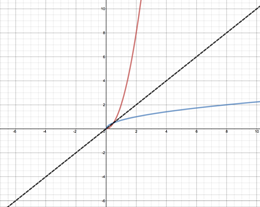
Step 2: Draw line y = x and look for symmetry.

If symmetry is not noticeable, functions are not inverses. If symmetry is noticeable double check with Step 3.

In this case symmetry is apparent so proceed to Step 3.

y = x

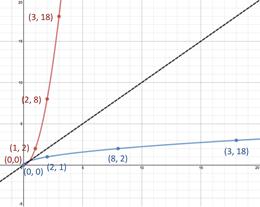
Step 3: Compare the coordinates of at least four points to see if the coordinates are reversed.

Since the four points selected show that the coordinates of f(x) are inverses of the coordinates of g(x) the functions are inverse functions.

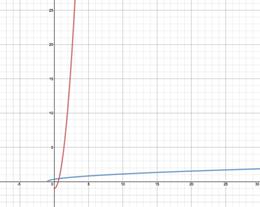
Example 2: Sketch the graphs of f(x) = 3x² - 1 and $g (x) = \frac{\sqrt{x + 1}}{3}$ for $x \geq 0$ and determine if they are inverse functions.

Step 1: Sketch both graphs on the same coordinate grid.

Step 2: Draw line y = x and look for symmetry.

If symmetry is not noticeable, functions are not inverses. If symmetry is noticeable double check with Step 3.

In this case symmetry is apparent so proceed to Step 3.

y = x

Step 3: Compare the coordinates of at least four points to see is the coordinates are reversed.

Since the four points selected show that the coordinates of f(x) are NOT inverses of the coordinates of g(x) the functions are NOT inverse functions. A closer look at the y = x line will reveal that it is a little of center.

To link to this Inverse Functions: Graphs page, copy the following code to your site:

<a href="https://www.softschools.com/math/pre_calculus/inverse_functions_graphs/">Inverse Functions: Graphs </a>

Inverse Functions: Graphs

More Topics

Educational Videos