Parametric Equations: Derivatives

Just as with a rectangular equation, the slope and tangent line of a plane curve defined by a set of parametric equations can be determined by calculating the first derivative and the concavity of the curve can be determined with the second derivative.

PARAMETRIC FORM OF THE DERIVATIVE:

If a smooth curve C is given by the continuous functions x = f(t) and y = g(t), then the slope of C and point (x, y) is as follows:

$\frac{d y}{d x} = \frac{\frac{d y}{d t}}{\frac{d x}{d t}}, w h e r e d y / d x \neq 0$ First derivative

$\frac{d^{2} y}{d x^{2}} = \frac{d}{d x} [\frac{d y}{d x}] = \frac{\frac{d}{d t} [\frac{d y}{d x}]}{\frac{d x}{d t}}$ Second derivative

Let's try a couple of examples.

Example 1:Find the slope and concavity of the curve represented by x = 2t and y = 3t - 1 at t = 4 and sketch the curve.

Step 1: Determine the first derivative of both parametric equations with respect to the parameter, $\frac{d x}{d t}$ and $\frac{d y}{d t}$ .

First parametric equation

x = 2t Original

$\frac{d x}{d t} = 2$ First derivative

Second parametric equation

y = 3t - 1 Original

$\frac{d y}{d t} = 3$ First derivative

Step 2: Substitute $\frac{d x}{d t}$ and $\frac{d y}{d t}$ into the parametric derivative equation for the first derivative and calculate the slope, $\frac{d y}{d x}$ .

$\frac{d y}{d x} = \frac{\frac{d y}{d t}}{\frac{d x}{d t}}$

$\frac{d y}{d x} = \frac{\frac{d y}{d t}}{\frac{d x}{d t}}$ 1 Deriv. Equation

$\frac{d y}{d x} = \frac{3}{2} = s l o p e$ Substitute

Step 3: Substitute $\frac{d y}{d x}$ and $\frac{d x}{d t}$ into the parametric derivative equation for the second derivative and determine concavity.

$\frac{d^{2} y}{d x^{2}} = \frac{d}{d x} [\frac{d y}{d x}] = \frac{\frac{d}{d t} [\frac{d y}{d x}]}{\frac{d x}{d t}}$

$\frac{d^{2} y}{d x^{2}} = \frac{d}{d x} [\frac{d y}{d x}] = \frac{\frac{d}{d t} [\frac{d y}{d x}]}{\frac{d x}{d t}}$ 2 Deriv. Equation

$\frac{d^{2} y}{d x^{2}} = \frac{\frac{d}{d t} [\frac{3}{2}]}{2}$ Substitute

$\frac{d^{2} y}{d x^{2}} = \frac{0}{2} = 0$ Take derivative

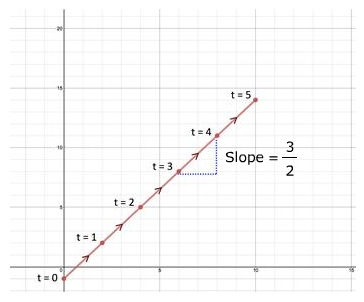
Step 4: Describe the graph at t = 4.

The slope and concavity of the plane curve at t = 4 is slope $= \frac{3}{2}$ and concavity does not exist.

Parametric Equations: x = 2t , y = 3t - 1

x = 2t

y = 3t - 1

-1

Example 2: Find the slope and concavity of the curve represented by $x = 3 \cos θ$ and $y = 3 \sin θ$ at $θ = \frac{π}{2}$ and sketch the curve.

Step 1: Determine the first derivative of both parametric equations with respect to the parameter, $\frac{d x}{d t}$ and $\frac{d y}{d t}$ .

First parametric equation

$x = 3 \cos θ$ Original

$\frac{d x}{d t} = - 3 \sin θ$ First derivative

Second parametric equation

$y = 3 \sin θ$ Original

$\frac{d y}{d t} = 3 \cos θ$ First derivative

Step 2: Substitute $\frac{d x}{d t}$ and $\frac{d y}{d t}$ into the parametric derivative equation for the first derivative and calculate the slope, $\frac{d y}{d x}$ .

$\frac{d y}{d x} = \frac{\frac{d y}{d t}}{\frac{d x}{d t}}$

$\frac{d y}{d x} = \frac{\frac{d y}{d t}}{\frac{d x}{d t}}$ 1 Deriv. Equation

$\frac{d y}{d x} = \frac{3 \cos θ}{- 3 \sin θ}$ Substitute

$\frac{d y}{d x} = - \frac{\cos θ}{\sin θ}$ Simplify

$\frac{d y}{d x} = - \cot θ$ Rewrite

$- \cot \frac{π}{2} = 0$ Find slope at $θ = \frac{π}{2}$

Step 3: Substitute $\frac{d y}{d x}$ and $\frac{d x}{d t}$ into the parametric derivative equation for the second derivative and determine concavity.

$\frac{d^{2} y}{d x^{2}} = \frac{d}{d x} [\frac{d y}{d x}] = \frac{\frac{d}{d t} [\frac{d y}{d x}]}{\frac{d x}{d t}}$

$\frac{d^{2} y}{d x^{2}} = \frac{d}{d x} [\frac{d y}{d x}] = \frac{\frac{d}{d t} [\frac{d y}{d x}]}{\frac{d x}{d t}}$ 2 Deriv. Equation

$\frac{d^{2} y}{d x^{2}} = \frac{\frac{d}{d t} [- \cot θ]}{- 3 \sin θ}$ Substitute

$\frac{d^{2} y}{d x^{2}} = \frac{\csc^{2} θ}{- 3 \sin θ}$ Take deriv.

Find concavity at $θ = \frac{π}{2}$

$\frac{\csc^{2} θ}{- 3 \sin θ} = \frac{\csc^{2} \frac{π}{2}}{- 3 \sin \frac{π}{2}} = - \frac{1}{3}$ Concave down

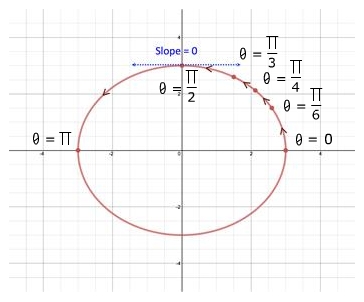
Step 4: Describe the graph at $t = \frac{π}{2}$ .

The slope and concavity of the plane curve at $t = \frac{π}{2}$ is slope = 0 and concavity is down.

Parametric Equations: $x = 3 \cos θ$ , $y = 3 \sin θ$

$\frac{π}{6}$

$\frac{π}{4}$

$\frac{π}{3}$

$\frac{π}{2}$

$x = 3 \cos θ$

$\frac{3 \sqrt{3}}{2}$

$\frac{3 \sqrt{2}}{2}$

$\frac{3}{2}$

-3

$y = 3 \sin θ$

$\frac{3}{2}$

$\frac{3 \sqrt{2}}{2}$

$\frac{3 \sqrt{3}}{2}$

Related Links:
Math
algebra
Inverse Functions: Graphs
Inverse Functions: One to One
Pre Calculus

To link to this Parametric Equations: Derivatives page, copy the following code to your site:

<a href="https://www.softschools.com/math/pre_calculus/parametric_equations_derivatives/">Parametric Equations: Derivatives</a>

Parametric Equations: Derivatives

More Topics

Educational Videos