Parametric Equations: Introduction

Parametric equations are equations that express two different variables in terms of a third variable called a parameter. Thus parametric equations come in pairs. The following set of parametric equations describe x, distance, and y, height, as a function of t, time. In this example the parameter is time.

$x = 40 t$

$y = - 16 t^{2} + 40 t$

To graph this set of parametric equations over the interval from time zero to time 2.5, create a table of values. Then determine the values for x and y by substituting the value of t in their respective equations.

Time, t

0.5

1.5

2.5

Distance, x
x = 40t

100

Height, y

y = -16t² + 40t

Graph the values on a xy-plane as normal, labeling each data point with the value of t.

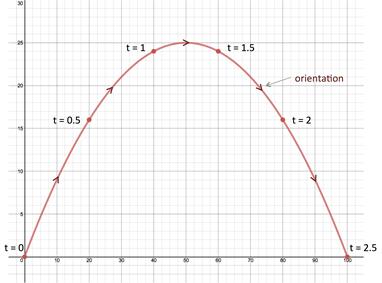
The graph shows that both x, distance, and y, height are continuous functions for t, time. This type of graph is called a plane curve.

The orientation of the plane curve is determined by the increasing values of the parameter. Therefore the orientation for the graph for our example starts at t = 0 and continues to the right as the values of t increase to t = 2.5, as shown by the arrows on the graph.

Let's try a couple of examples.

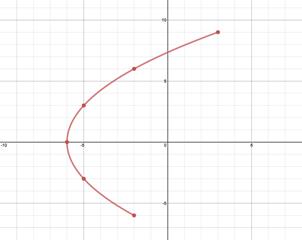
Example 1: Sketch the curve for the parametric equations when $- 3 \leq t \leq 3$ and indicate the orientation of the curve.

x = t² - 6
y = 3t

Step 1: Create a table of values for the interval $- 3 \leq t \leq 3$ .

-3

-2

-1

x = t² - 6

-2

-5

-6

-5

-2

y = 3t

-9

-6

-3

Step 2: Plot the points.

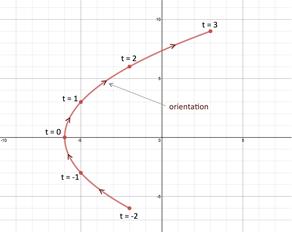
Step 3: Indicate orientation.

The orientation is shown in the graph in the direction of increasing values for the parameter, t.

Notice that x does not have to be a function of y (The graph does not pass the vertical line test). Therefore parametric curves can be drawn for more than just functions.

In fact two different sets of parametric curves can represent the same plane curve.

Example 2: Sketch the curve for the parametric equations when $- 2 \leq t \leq 2$ and indicate the orientation of the curve.

$x = \frac{t}{3}$

$y = t^{2}$

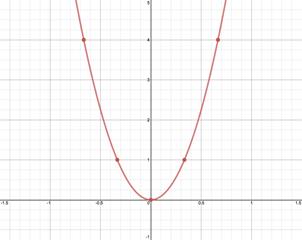
Step 1: Create a table of values for the interval $- 2 \leq t \leq 2$ .

-2

-1

$x = \frac{t}{3}$

$- \frac{2}{3}$

$- \frac{1}{3}$

$\frac{1}{3}$

$\frac{2}{3}$

y = t²

Step 2: Plot the points.

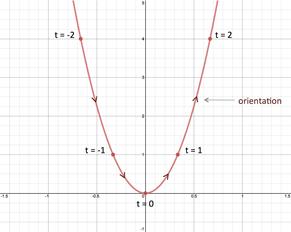
Step 3: Indicate orientation.

The orientation is shown in the graph in the direction of increasing values for the parameter, t.

Point plotting parametric equations works well when given a small finite interval for the parameter. When the interval is not small and finite, point plotting can be very tedious. This situation is managed by eliminating the parameter. This concept is discussed as a separate topic.

To link to this Parametric Equations: Introduction page, copy the following code to your site:

<a href="https://www.softschools.com/math/pre_calculus/parametric_equations_introduction/">Parametric Equations: Introduction</a>

Parametric Equations: Introduction

More Topics

Educational Videos