Measures of Center: Mean, Median, and Mode
Measures of center generally tell us about the middle, or center, of a distribution. They are the mean, the median, and the mode. Each plays a useful role in Statistics.
The Mean
The mean, or arithmetic average, is calculated by adding all the data values and dividing by the number of values. Symbolically, this is expressed as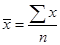
, where
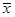is the statistical symbol for the mean,
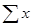is the sum of the data values, and n is the number of values.
For example you are given the following data values: 3, 7, 8, 11, 11. To calculate the mean, first add the values: 3 + 7 + 8 + 11 + 11 = 40. Then divide by the number of values, n, which is 5. From the formula we have: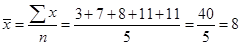
. Thus, the mean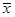= 8.
The Median
When any set of numbers is placed in numerical order, the median is the value that is in the middle of the arranged set. Half of the numbers in the set are above the median and half are below the median.
For the data set 3, 7, 8, 11, 11, note that the five data values are already arranged in order. Now simply pick the middle number, which is 8; this is the median. There are two data values above it and two data values below it.
Now consider what would happen if we had another data set: 2, 6, 8, 9, 14, 16. There is no data value that is exactly the middle number. In this case, we pick the two middle numbers and average them to determine the median: 2, 6, 8, 9, 14, 16. The median is the average of 8 and 9, and thus, the median is 8.5.
We can summarize the two examples above by noting that if you have a data set with an odd number of data values, the middle value of the ordered set is the median. But if you have a data set with an even number of data values, you must choose the two middle values and find their average to determine the median.
The Mode
The mode is the most frequently occurring data value. For the data set 3, 7, 8, 11, 11, the mode is 11, because the value 11 occurs twice, whereas all the other values occur only once. For a data set like 2, 6, 8, 9, 14, 16, we say that there is no mode, because no data value occurs more than any other data value.
The Mean
The mean, or arithmetic average, is calculated by adding all the data values and dividing by the number of values. Symbolically, this is expressed as
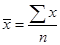, where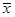is the statistical symbol for the mean, 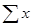is the sum of the data values, and n is the number of values.For example you are given the following data values: 3, 7, 8, 11, 11. To calculate the mean, first add the values: 3 + 7 + 8 + 11 + 11 = 40. Then divide by the number of values, n, which is 5. From the formula we have:
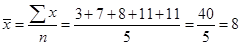. Thus, the mean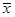= 8.The Median
When any set of numbers is placed in numerical order, the median is the value that is in the middle of the arranged set. Half of the numbers in the set are above the median and half are below the median.
For the data set 3, 7, 8, 11, 11, note that the five data values are already arranged in order. Now simply pick the middle number, which is 8; this is the median. There are two data values above it and two data values below it.
Now consider what would happen if we had another data set: 2, 6, 8, 9, 14, 16. There is no data value that is exactly the middle number. In this case, we pick the two middle numbers and average them to determine the median: 2, 6, 8, 9, 14, 16. The median is the average of 8 and 9, and thus, the median is 8.5.
We can summarize the two examples above by noting that if you have a data set with an odd number of data values, the middle value of the ordered set is the median. But if you have a data set with an even number of data values, you must choose the two middle values and find their average to determine the median.
The Mode
The mode is the most frequently occurring data value. For the data set 3, 7, 8, 11, 11, the mode is 11, because the value 11 occurs twice, whereas all the other values occur only once. For a data set like 2, 6, 8, 9, 14, 16, we say that there is no mode, because no data value occurs more than any other data value.
|
Related Links: Math Probability and Statistics Percentiles and Quartiles Boxplot (Box and Whiskers Diagram) |
To link to this Measures of Center: Mean, Median, and Mode page, copy the following code to your site: