Measures of Spread: Range, Standard Deviation, and Variance
When we view a data set, we often want to know whether all of the data points are close together or are spread far apart (or something in between). For example, imagine asking 15 adults how many teeth they have. We'd probably see that most people have about 32 teeth. Some may have 29, some 30, some 31, but most will have 32 teeth. In analyzing this data, we'd say that there was not much variation in the data because most of the data points were all grouped together.
However, if we instead measured the IQ of each of those 15 adults, we'd likely see a data set that had IQ scores ranging roughly from 80 to 120, and furthermore, we'd likely see that the IQ scores were spread out. For example, we may see scores such as 82, 84, 86, 89, 90, 91, 93, 95, 99, 101, 103, 110, 114, 119, 120. Notice that this data set would be much more spread out. We'd say that this data set has a greater variability. In other words, in this data set, some of the data values are relatively far from the mean.
You must be familiar with two simple measures of variability: range and standard deviation.
Range
The range is a simple measure of how spread out a set of data is as a whole. The formula for the range is: Range = Highest Number in the Set - Lowest Number in the Set. For the IQ data above, the range is: Range = 120 - 82 = 38.
Standard Deviation
Much like the range, standard deviation measures the dispersion, or spread, of values in a data set. More specifically, standard deviation measures how far the data points are from the mean of the data set. In general, a higher standard deviation results when most points in a data set are far from the mean, and a lower standard deviation results when most points in a data set are close to the mean. In fact, if all of the values in the data set were the same, the standard deviation would be zero. That is, there would be no difference between any of the terms and the mean.
The calculation of the standard deviation is rather complicated, but you need to understand its use. In general, the more spread out the data are, the greater the standard deviation. Consider these two simple charts:
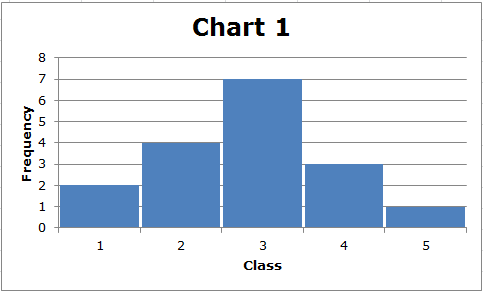
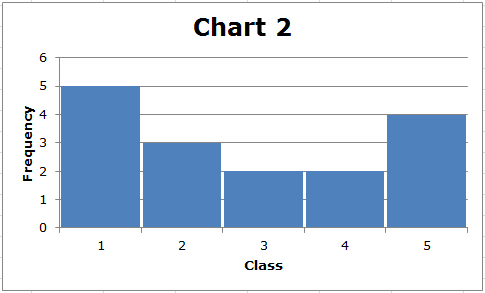
First, notice that the range of each data set is (5-1) = 4. However, the standard deviation of the data displayed in Chart 2 is greater than the standard deviation of the data displayed in Chart 1. We can see this visually. In Chart 1, the data are clustered about the middle, whereas in Chart 2, there are fewer data values in the middle, and most of the data values are relatively far from the middle. In general, the farther data points are from the middle of the distribution, the greater the standard deviation.
Variance
The variance is the square of the standard deviation. For example, if the standard deviation is 15, then the variance is (15)2 = 225. In basic statistics, the variance is seldom used, but in some advanced applications, it is used extensively.
However, if we instead measured the IQ of each of those 15 adults, we'd likely see a data set that had IQ scores ranging roughly from 80 to 120, and furthermore, we'd likely see that the IQ scores were spread out. For example, we may see scores such as 82, 84, 86, 89, 90, 91, 93, 95, 99, 101, 103, 110, 114, 119, 120. Notice that this data set would be much more spread out. We'd say that this data set has a greater variability. In other words, in this data set, some of the data values are relatively far from the mean.
You must be familiar with two simple measures of variability: range and standard deviation.
Range
The range is a simple measure of how spread out a set of data is as a whole. The formula for the range is: Range = Highest Number in the Set - Lowest Number in the Set. For the IQ data above, the range is: Range = 120 - 82 = 38.
Standard Deviation
Much like the range, standard deviation measures the dispersion, or spread, of values in a data set. More specifically, standard deviation measures how far the data points are from the mean of the data set. In general, a higher standard deviation results when most points in a data set are far from the mean, and a lower standard deviation results when most points in a data set are close to the mean. In fact, if all of the values in the data set were the same, the standard deviation would be zero. That is, there would be no difference between any of the terms and the mean.
The calculation of the standard deviation is rather complicated, but you need to understand its use. In general, the more spread out the data are, the greater the standard deviation. Consider these two simple charts:


First, notice that the range of each data set is (5-1) = 4. However, the standard deviation of the data displayed in Chart 2 is greater than the standard deviation of the data displayed in Chart 1. We can see this visually. In Chart 1, the data are clustered about the middle, whereas in Chart 2, there are fewer data values in the middle, and most of the data values are relatively far from the middle. In general, the farther data points are from the middle of the distribution, the greater the standard deviation.
Variance
The variance is the square of the standard deviation. For example, if the standard deviation is 15, then the variance is (15)2 = 225. In basic statistics, the variance is seldom used, but in some advanced applications, it is used extensively.
|
Related Links: Math Probability and Statistics The Normal Distribution - Empirical Rule Normal Distribution - Simple Probabilities |
To link to this Measures of Spread: Range, Standard Deviation, and Variance page, copy the following code to your site:
