Irrational Numbers
Recall that rational numbers can be written as a fraction.
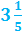, 0.55555 = 
, -20 =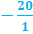 
Some famous examples of irrational numbers would include
However, there are many more examples of irrational numbers. In fact, many square roots fall into the irrational category.
Examples:
- Irrationals numbers cannot be written as a fraction. If you try to write them out in decimal form, they do not end, or terminate, and they do not repeat. There might be a pattern after the decimal but it won't repeat.
For example:
3.4848484848484848484.... is rational because the digits repeat.
5.12112211122211112222.... is irrational because it has a pattern, but the same numbers do not repeat over and over.
- When you add two irrational numbers, you always get an irrational number.
For example:
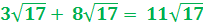
- However, when you multiply irrational numbers you will sometimes get a rational number as the product.
For example:
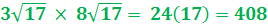
Irrational numbers are used in many different mathematical topics. It is believed that one of Pythagoras's students actually proved that there were irrational numbers when a proof showed that √2 could not be written as a fraction.
Today, we can use irrational numbers when determining the length of the hypotenuse in a right triangle using the Pythagorean Theorem.
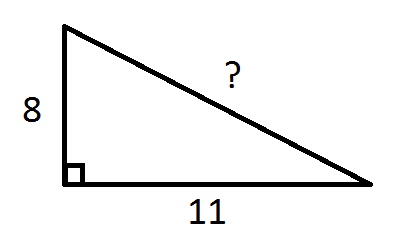
a2 + b2 = c2
82 + 112 = c2
64 + 121 = c2
√185 = c
Let's Review
Irrational numbers are Real, but they cannot be written as a fraction. Pi, Euler's number and many square roots are examples of irrational numbers. The irrational numbers do not end and do not repeat. They are useful when determine circumference or area of circles, in the many applications of Euler's number and whenever square roots are used, just to name a few!
Related Links:
Math
algebra
Euler's Number
To link to this Irrational Numbers page, copy the following code to your site: