Rational Numbers are part of the Real Number System. Rational numbers are special because they can be written as a fraction.



More specifically, the definition of rational numbers says that any rational number can be written as the ratio of p to q, where p and q are integers and q is not zero.

Examples

Rational numbers are often numbers you use every day. You might notice that many numbers can be written as a fraction.



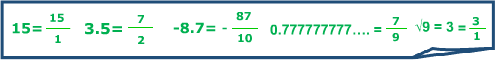
Not all numbers are rational. Numbers like √7 or 0.2810582107432.... are not rational because they cannot be written as fractions. In addition, numbers like 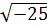are also not rational because they are not real.Not all numbers are rational. Numbers like √7 or 0.2810582107432... are not rational because they cannot be written as fractions. In addition, numbers like 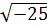are also not rational because they are not real.

So here are the basics: When a rational number is written in decimal form, the number will terminate (or end) or it will repeat. If the decimal does one of these two things, it can be written in fraction form.

Be Careful:

6.343434343434.... is a repeating decimal. It can be written as a fraction 6

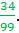
However, 6.34334433344433334444... is not a repeating decimal. It does have a pattern, but the 34 does not repeat over and over. Therefore, this is not a rational number.

Why are Rational Numbers Important?

Ancient Greek mathematicians thought that all things could be measured using rational numbers. So when the Pythagorean Theorem came into play and showed that some lengths could not be written as a rational number, their whole idea of numbers was changed.

The Ancient Greeks were kind of right! Rational numbers are used all the time! From buying and selling products using money and terminating decimals to cooking with fractions, people use rational numbers just about every day! In addition, by giving the group of numbers a name and characteristics, we can study them, learn about their properties and even expand our horizon to determine what other types of numbers are used when rational numbers don't get the job done.


Related Links:
Math
algebra
Irrational Numbers