It is not always necessary to find a reference angle to calculate the sine, cosine, and tangent of large or negative angles. Recall in the coordinate plane that:



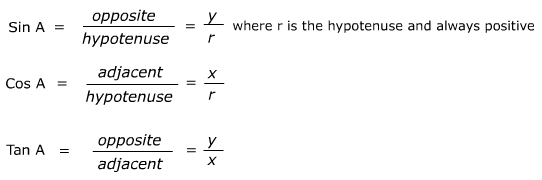
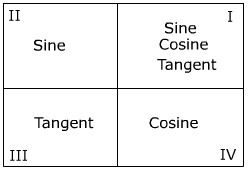
This leads to the functions being positive in the following quadrants.



Let's look at an example of a large angle. Consider the following graph of a 200° angle. A right triangle is created using the x axis and the terminal side of the angle.



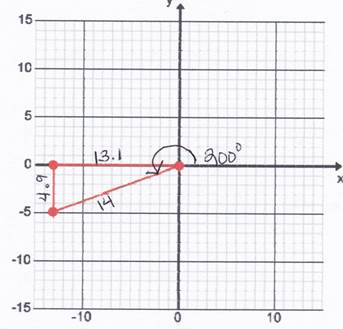
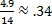Therefore sin 200° 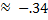Because sine is negative in Quadrant III.

Let's look at an example of a negative angle. Consider the graph of a -31° angle. A right triangle is created using the x axis and the terminal side of the angle.



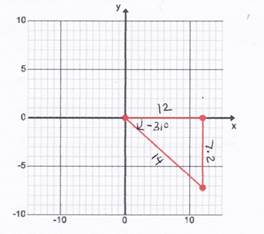
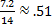Therefore sin -31° 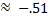Because sine is negative in Quadrant IV.

Notice that the sine ratio still holds true with only a variance in sign based on the quadrant in which the terminal side of the angle lies. The same will also apply to the other trig ratios: cosine, tangent, secant, cosecant and cotangent.

Related Links: Math Trigonometry Inverse Trigonometric Functions Quadrantal Angles