Pythagorean Identities
Let's look at how it works. Given the unit circle, which has a radius of 1, and any point on the circle that creates the vertex of a right triangle can be represented by the coordinates (x, y)
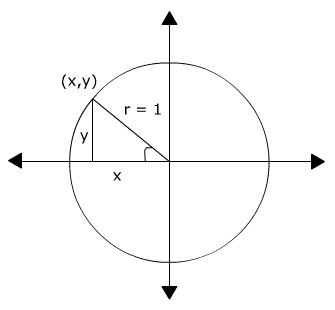


Recall the Pythagorean Theorem is x2 + y2 = c2. Since the legs of the right triangle can be represented by sin θ and cos θ and the radius is the hypotenuse we can use the Pythagorean Theorem to derive sin2 θ + cos2 θ = 1.
From this fundamental identity we can derive equivalent identities such as:
- sin2 θ + cos2 θ = 1
- sin2 θ + cos2 θ = 1
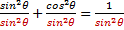 using the division property of equality
using the division property of equality
-cos2 θ -cos2 θ using the subtraction property of equality
| sin2 θ = 1 - cos2 θ |
-sin2 θ -sin2 θ using the subtraction property of equality
| cos2 θ = 1 - sin2 θ |
1 + cot2 θ = csc2 θ use substitution
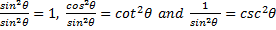
-1-1use subtraction property of equality
| cot2 θ = csc2 θ - 1 |
Deriving the Pythagorean identities leads to understanding the basic trigonometric proofs. Recall that when solving an equation both sides of the equation may be manipulated to find a solution. However, when proving an identity only one side of the identity may be manipulated.
|
Related Links: Math Trigonometry Cofunction Identities Sum and Difference of Angles Identities |
To link to this Pythagorean Identities page, copy the following code to your site:
