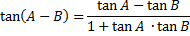Sum and Difference of Angles Identities
|
Sum of Angles Identities |
Difference of Angles Identities |
|
sin(A + B) = sin A · cos B + cos A · sin B |
sin(A - B) = sin A · cos B - cos A · sin B |
|
cos (A + B) = cos A · cos B - sin A · sin B |
Cos(A - B) = cos A · cos B + sin A · sin B |
|
tan (A + B) =
|
|
Example: find the exact value of cos of 75° using a sum formula.
Since 75 is the sum of 30 and 45 the cos sum formula can be used.
cos (A + B) = cos A · cos B - sin A · sin B
cos (30 + 45) = cos 30 · cos 45 - sin 30 · sin 45
= 
= 
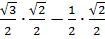
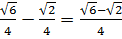
Therefore cos 75° =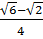 
Example: find the exact value of the sine of 15° using a difference formula.
Since 15 is the difference of 45 and 30 the sine difference formula can be used.
sin(A - B) = sin A · cos B - cos A · sin B
sin(45 - 30) = sin 45 · cos 30 - cos 45 · sin 30
= 
=
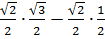
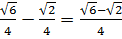
Therefore sin 15° =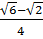
3 special notes:
1) You may have more than one option. For instance find the sine of 120°
sin(90 + 30) using the sum formula
or
sin(180 - 60) using the difference formula
both formulas will yield the same result.
2) Remember to determine in which quadrant the angle will lie. Using the sine of 120° from above the final answer will have to be negative because 120° is in quadrant II and sine is negative in quadrant II.
3) To find a cosecant, secant or cotangent function you change the expression to one of the three basic functions, do the necessary calculations. Then use the reciprocal identity again to change the answer back to the original identity. For example to find csc 15° we can look at the example above for the sin 15° because sine and cosecant are reciprocals.
sin 15° = 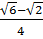therefore csc 15° = 
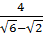(which will need to be rationalized)
|
Related Links: Math Trigonometry Trigonometric Identities - Reciprocal Identities Coterminal Angles |
To link to this Sum and Difference of Angles Identities page, copy the following code to your site: