Let's start with the simple right triangle reciprocal identities. Recall from Algebra that when a number is multiplied by its reciprocal the result is a product of 1. For Example:



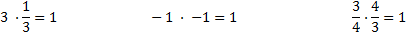
The six right triangle reciprocal identities are defined below.

Let's use sine and its reciprocal, cosectant, as an example of how the identities work:

     sin 30° = csc 30° = 2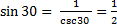

are reciprocals therefore sin and cosecant are reciprocals.

The question that begs to be asked is "What is the difference between an equation and an identity?" The answer is that an equation is only true for certain values of the variable and an identify is true for ALL values of θ. For Example:

In the equation 3x + 9 = 18 there is only one value of x that will make this statement true: x = 3

However, when we replace θ with a variety of values such as:

   

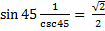
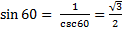
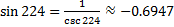
we see that regardless of the value of θ the identity will be a true statement. The importance of an identity will become more apparent in the applications of calculus where using an identity will give an expression a more convenient form.

Related Links: Math Trigonometry The Tangent Function in Right Triangles Quotient Identities Pythagorean Identities