Tangent is a trigonometric ratio comparing two sides of a right triangle. Tangent is usually shortened to tan but is pronounced tangent. This function can be used to determine the length of a side of a triangle when given at least one side of the triangle and one of the acute angles.

Quick Review: the three main trig ratios are sine, cosine and tangent. They can be memorized using SOH CAH TAH What does this mean? It means that tangent is the ratio of the opposite side divided by the adjacent side.

Tanθ =

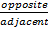
Let's look at an example at how tangent can be used to find the length of the opposite side.



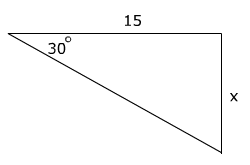
To find x write an equation using the tangent ratio and then solve for x

tan 30° = 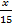multiply both sides of the equation by 15

(15) tan 30 = 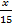(15) You will need to use a calculator to find the value of tan 30°

(15) (.5774) = xmake sure your calculator is in degree mode by verifying that tan 30 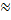.5774 (rounded to 4 decimal places)

8.661 = xThe opposite side has an approximate length of 8.661 or 8.7 if rounded to the nearest tenth.

Now let's look at how Tangent can be used to find the length of the adjacent side.



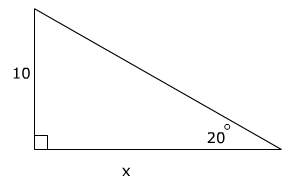
To find x write an equation using the tan ratio and then solve for x

Tan 20° = 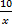Multiply both sides of the equation by x.

(x) tan 20° = 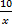(x)You will need to use a calculator to find the value of tan 20°. Round to 4 decimal places

Make sure your calculator is in degree mode by verifying that (x) (.3634) = 10     tan 20 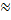.3634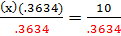

Divide both sides by .3634 to isolate x

x = 27.5179Round your answer to the nearest tenth

x = 27.5    the length of the adjacent side is approximately 27.5

The trig ratios have many real world and practical applications in fields such as aviation, architecture, surveying. Using the trigonometric ratios, such as tangent, allows for the measurement of things that cannot be determined using typical measurement tools.

Related Links: Math Trigonometry Graphing the Cosine Function Cotangent, Secant and Cosecant